關于聚類分析,在之前《多元分析》中有提及到。聚類分析有很多種方法,層次聚類、kmeans聚類等等。今天和大家分享一下層次聚類(也叫“系統聚類”)的概念以及應用。
01、層次聚類簡介
我們知道,聚類分析是把相似的個體聚在一起。那么具體我們應該按照什么樣的規則來聚類呢?
關于層次聚類,具體可以從兩個方向來考慮:凝聚法和分離法。
(1)凝聚法
凝聚法,顧名思義,就是逐步的凝聚在一起。
換句話說,我們是從單個的個體出發的,逐步合并最“相似”的個體,直到所有的個體都合并為一個族群。
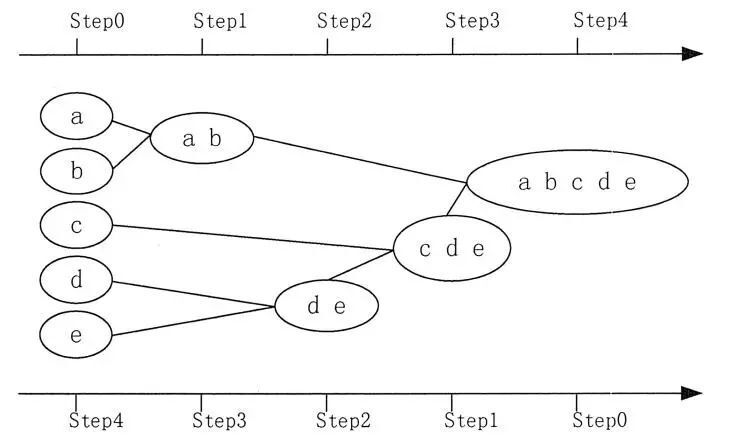

具體步驟如下:
- 步驟一:先把n個樣本當成n個不同的族群
- 步驟二:計算n個族群間的距離矩陣
- 步驟三:合并距離最小的兩個族群,計算新的族群間的距離矩陣
- 步驟四:如果族群數為1,則到步驟5,否則到步驟3
- 步驟五:繪制系統樹圖
- 步驟六:選擇族群個數
(2)分離法
分離法,其實是凝聚法的相反方向。
顧名思義,分離法是先把所有的個體看成是一個族群,慢慢分到n個完全不同的族群。
下面,我們這里重點對凝聚法進行分享。
02、凝聚法詳情
根據上面的概述我們知道,凝聚法的每一步需要合并“距離最小的兩個族群”,而不同族群間距離的定義方法決定了不同的聚類結果,關于凝聚法的距離定義主要有兩種思想:連接法和Ward法。
(1)凝聚法之——連接法
連接法又細分了以下四種:


- 簡單連接:定義兩族群間相隔最近的兩個個體間的距離,為兩族群的距離
- 完全連接:定義兩族群間相隔最遠的兩個個體間的距離,為兩族群的距離
- 平均連接:A群中所有的Na個樣本與B群中所有的Nb個樣本產生的距離(共計Na*Nb個距離),求平均值,作為兩個族群的距離
- 質心連接:兩個群中各自的質心(即樣本均值向量),之間的歐式距離,作為兩個族群的距離
上面的幾種方法可以通過下圖來理解:


上圖中分別是:簡單連接、完全連接、平均連接、質心連接。
平均連接法和質心連接法的區別在于,平均連接是先將兩族群間所有的距離求出來,然后求均值;而質心法是先求族群內所有樣本的平均質心,然后看質心距離。
質心法看著更加合理一些,但也是有一些局限的。比如其他三種方法,其實都是單調的(即每一步聚類步驟,都是可以基于之前的距離計算的,不需要重復計算),但質心法是非單調的,有可能出現距離的反復。
另外,由于質心法是所有樣本的平均,所以容易受到樣本量的影響,聚類后的新的群組質心會出現傾斜。改進的方法是不加權,基于原有兩個群的質點連線的中點作為新質心。
(2)凝聚法之——Ward法
連接法是基于兩個族群樣本間距離作為族群距離,與其不同的是,ward法其實是通過合并前后的族群內方差平方和的差異,來定義群組距離的。
有以下公式:
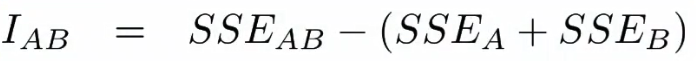

A、B代表了合并之前的兩個族群,AB代表了合并之后的族群。I-AB代表合并前后的SSE的差異。關于SSE,就是和方差,回頭系統講講。
啥意思呢?其實很好理解。如果兩個族群比較近,那么合并以后的方差應該也不是很大,因為方差衡量的是離散程度。
但Ward法有一個問題就是,更傾向于合并小的族群。因為大的族群從方差層面,肯定是容易比小族群大的。
03、繪制系統樹圖
其實根據上面的簡介,我們能夠了解到,所謂的層次聚類,是一種聚類的路徑。那如何利用圖表表示層次聚類的過程呢?
對,這就是系統樹圖。看一個示例圖:
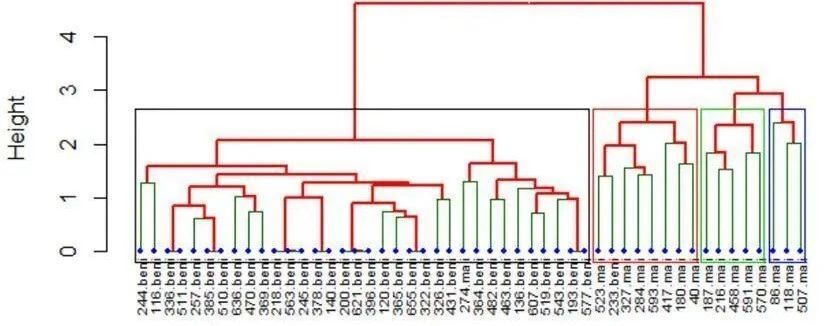

上圖就是一個典型的系統樹圖,很好地呈現了整體的聚類過程。
根據上面的系統樹圖,我們可以看出每一步的聚類過程,包括合并族群帶來的距離的變化。最底下是所有的待聚類的所有個體,縱軸就是聚類的距離。逐步往上,是一次次的聚類過程。最上面,就是一個類別了。
除了上面這種比較典型的系統樹圖的呈現外,也有下面的變形:
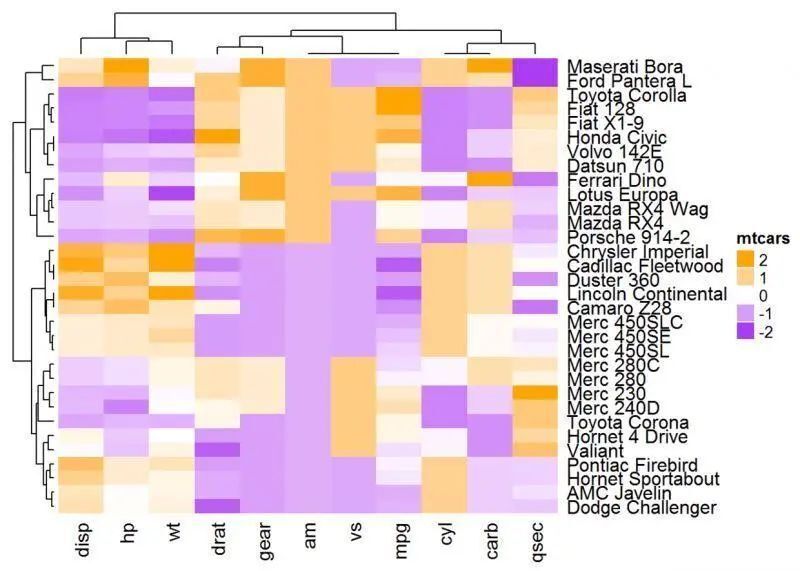

這種系統樹圖,多在基因的聚類分析中看到。該圖包括了兩個維度的聚類,一方面是樣本的聚類,另一方面是變量(基因信息)的聚類。
04、族群個數的選擇
還有最后一個問題,就是我們應該選取多少個族群呢?
單純從系統樹圖上看,在不同距離上截取,是可以選擇不同族群的。看下面兩個圖:
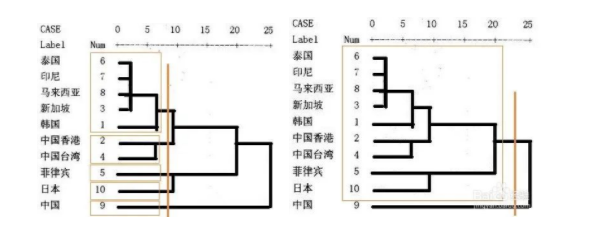

當我們在不同距離上截取時,聚類的個數也不同。左邊的圖聚成5類,而右邊的圖聚成2類。那到底應該選取幾個族群合適呢?
這個其實是比較主觀的一個過程了。
一方面,可以根據業務情況或者經驗,選擇比較好解釋的聚類;另一方面,也可以通過數據層面,尋找組別差距比較大的距離變化的節點。
另外,從上面的過程中,我們也可以看出來,層次聚類是一個單向的過程,一旦一個個體被分入到某一個群體之后,就沒有辦法歸入到其他群體了。這也決定了層次聚類只能達到局部最優的這樣一個結論,而一般不可能是全局最優。這是層次聚類的一個很大的缺點。
本文為@運營喵原創,運營喵專欄作者。